About

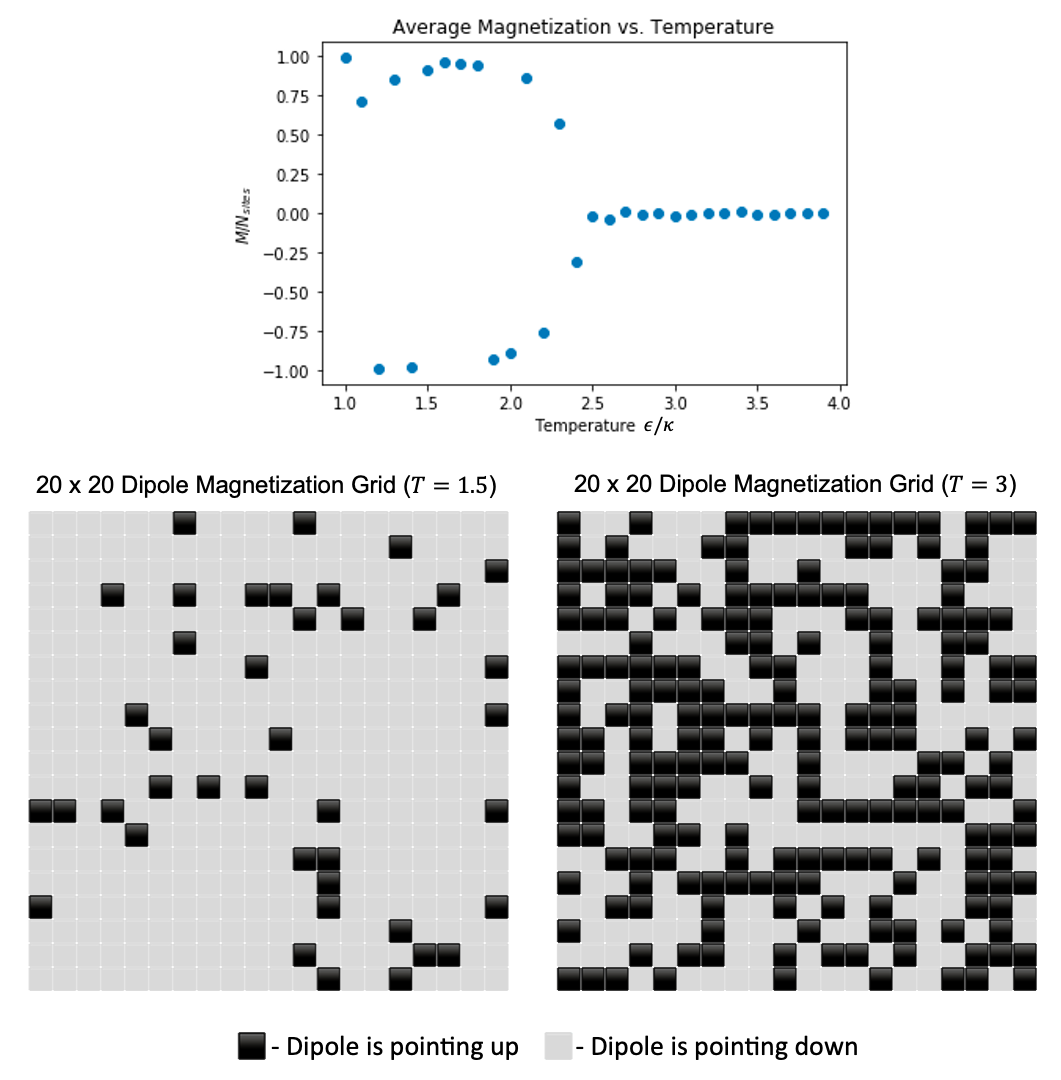
The Ising model attempts to model the behavior of a ferromagnet in the absence of an external magnetic field. In particular, this model takes into account the tendency for neighboring dipoles in a lattice to align parallel to each other, and the model assumes that each dipole can only point either up or down.

This project investigates the Ising model for different lattices, including a square, triangular, hexagonal, and random lattices, and it uses a Monte Carlo simulation to find the critical temperature (the point at which the lattice changes from having some net magnetization to zero net magnetization) for each lattice.

How was it built?

Everything was written in a Jupyter Notebook using Python.

Challenges faced

The hardest part of the simulation was figuring out how to model the different lattices. Each node in the Ising model is placed in a 2D NxN array, and the challenge was figuring out what each neighbor is. Some lattices, like the square or triangular lattice, were easy to figure out, but others, like the hexagonal lattice, took more time.

Results

Here are the results for some of the lattices I used. The critical temperature is the first data point, when going left to right, where the average magnetization is zero. Note: for temperatures below the critical temperature, the average magnetization seem to be either +1 or -1, and this just means the majority of the dipoles are either pointing up or down.

Conclusion

The overall trend, based on my results, is the more neighbors a dipole has the higher the critical temperature.